談技術：如何用 DAG 最短路徑演算法取消組字區字數上限

小麥注音 2.4 版取消了組字區字數上限。這是怎麼做到的？我們很少談論小麥的技術細節，在此轉錄先前貼在 Twitter 上的推文串做個說明。

首先簡單描述小麥注音的選字原理。小麥選字引擎的主要任務是回答以下問題：「輸入一串注音，最有可能輸出什麼中文字詞？」要回答這問題，選字引擎先根據辭典將同音字詞節點組成圖，再用簡化的 n-gram 模型進行最大概然估計 (maximum likelihood estimation) ，找出最有可能的路徑。

舉例來說，「台灣的語言與文化」有好幾種走法。可以是「台灣 的 語言 語文 化」，但如附圖所示，「台灣 的 語言 與 文化」更有可能。如下圖所示：

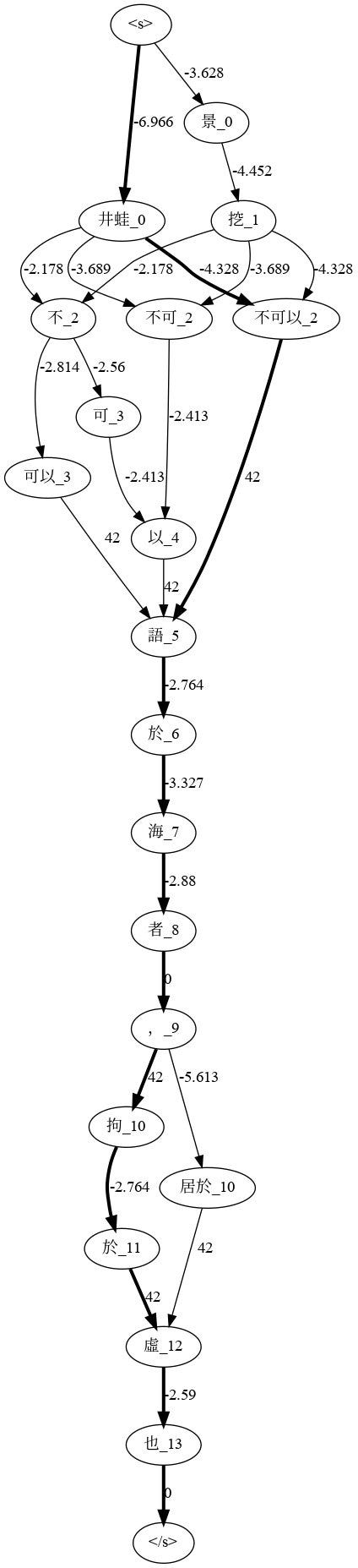
如果使用者手動選字，我們就刻意挑使用者選取的字詞節點走。例如，「井蛙不可以語於海者，拘於虛也」在選字後的走法是：

搜尋最短路徑不是什麼複雜的演算法。但以往小麥注音在這方面，寫得不是很好…… 原來的演算法走了許多不必要的路徑，節點一多就顯得慢。當時我們把組字區限制在十字以內，超過了就送出組字區開頭第一詞，因此游刃有餘。

但這招在開發 Linux 版時碰到了問題：許多應用程式不喜歡輸入法在組字狀態下逕行輸出部分文字。

於是我們開始討論要不要取消組字區長度限制、該怎麼取消…… 小麥注音 2.3 版對原有的演算法做了許多調整，將長度限制拉到一百個字。另一方面，今年以來我們做了不少 C++ 程式碼的整理與重構，讓我們有機會思考要不要翻新小麥注音的核心程式碼。

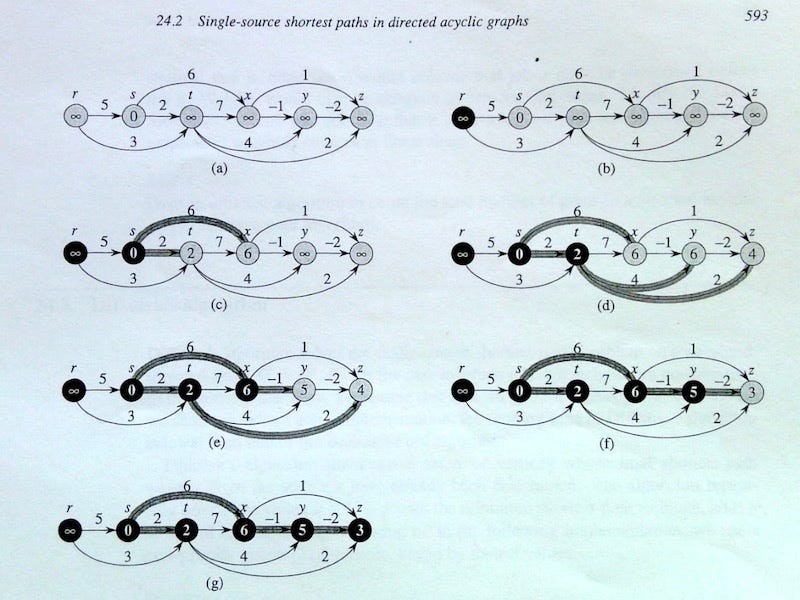
原本在想，是不是把課本找出來，寫個 Dijkstra 演算法就好？這是求最短路徑最標準的作法。結果我們在複習課本的時候，發現了以前沒注意的段落……

上面兩圖取自經典教科書 Cormen et al. 2001. 這裡說的是，如果你的圖是 DAG (Directed Acyclic Graph; 有向非循環圖)，最短路徑可以快速找出，根本不需要 Dijkstra!

於是我們重寫了這部份的程式。因為這是個 Θ(V + E) 演算法 (V 是節點數，E 是邊數)，組字區就算放了幾百字，普通筆電也能在千分之一秒內計算完成。

我們趁機檢視過去定義的資料結構，汲取新版 C++ 的特長，還因此修正了過往一些選字後，仍無法正確取代當前字詞的問題。

組字區字數限制取消後，輸入法不再需要動態輸出過長的部分，程式碼因而簡化不少，功能的提升改進更是自不待言，堪稱一輪饒富興味的工程。